Olbers' Paradox: The Math

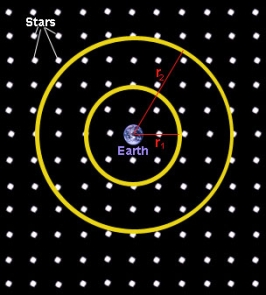
In the above figure, more stars lie on the larger (r₂) circle than on the smaller (r₁) circle.

The amount of light we see from stars some distance r from Earth can be calculated by multiplying the number of stars N that distance away, multiplied by the intensity I of each star.

N increases as r² increases since N = constant × r²

The intensity of light follows the Inverse-Sqaure Law:

I = constant × 1/r²

Multiplying N and I cancels r² with 1/r², leaving a constant value for the intensity at some distance r. However, since the Universe is infinite, this constant value must be added an infinite number of times, implying that the Universe must be infinitely bright. This is obviously not true: if you look at the sky at night, you can see clearly defined individual stars with regions of darkness between them - the sky is not brightly illuminated everywhere. This apparent contradiction is the essence of Olbers' Paradox. Why, then, is the night sky dark? What is the solution to Olbers' Paradox?