Working Towards A Solution

We learned earlier, from Hubble'’s Law, that stars further away from us recede more quickly than closer stars--that is, they have a higher recession velocity. Consequently, these stars are more redshifted than those closer to us. Since redshift is caused by an increase in wavelength, it is possible that distant stars have been so redshifted that the light they emit is no longer in the visible light part of the spectrum, so we see no light coming from these stars, accounting for the dark regions of the night sky. This solution for Olbers'’ Paradox requires that the universe is expanding--evidence for the Big Bang.

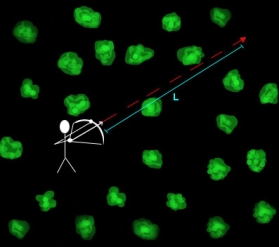
Since the arrow's mean free path (L) is larger than the radius of the forest, not all of the archer's arrows will hit a tree. This explains how, since L is longer than the radius of the observable universe, not all of the sky we see at night is covered by stars.

The mean free path L, or distance our line of sight can travel before hitting a star (or how far you could shoot an arrow before it would hit a tree in the forest analogy from earlier) is given by the equation:

L = V/A

Where A is the cross-sectional area of the star and V is the "volume owned" by a star.

A = π × (radius of the star)² ≈ 10^22.5 cm² and
V = (mass of star) × (average density) ≈ 10⁶³ cm³

Dividing V by A, we find that L is approximately 3.16 × 10⁴⁰ cm or 3 × 10¹³ billion light years.

Imagine separating all of the stars in the universe into separate cells so that every point in a cell is closer to that cell's star than to any other star. The volume of an average cell is the "volume owned".

Of what use is this result? Read on to find out!