The Flatness Problem

Spatial geometry depends upon the ratio of the Universe's total mass density to its critical density and is denoted Ω_tot . Conservative estimates place this value within the range 0.5 ≤ Ω_tot ≤ 1.5, implying that the Universe is very close to possessing a Euclidean geometry (Ω_tot = 1). If Ω_tot is exactly equal to one then space is flat and Ω_tot will remain constant. However Ω_tot can vary with time if its value is slightly higher or slightly lower than one. In fact the expansion of the Universe will quickly drive Ω_tot away from one if there is any slight initial curvature. A flat Universe is a highly unstable one.

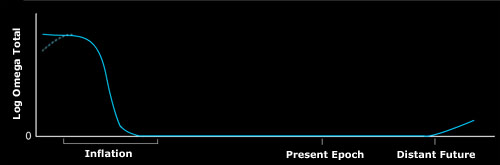
If Ω_tot is driven away from one by expansion, why is the current estimated value so close to one? The solution to the flatness problem is inflation. Inflationary theory entails that for a brief time the Universe rapidly expanded, causing the Universe to appear flatter and driving Ω_tot towards one. The resulting value was so close to one that subsequent periods of expansion have yet to cause it to diverge.