Standard Candles
It is easy to measure the intensity (observed brightness) of an object from Earth, but how do we know the luminosity (intrinsic brightness) of the object? There are certain objects whose luminosity is always the same no matter where they appear in the universe, and we can use that fact to determine their distance from Earth.
These types of objects are called "standard candles". To measure distances across the universe, we need objects that are incredibly bright (so we can see them). For this reason astrophysicists use a particular type of supernova that always has the same peak luminosity. Type Ia supernovae are easily identified by their characteristic explosion, and at their brightest, they are almost as bright as an entire galaxy.
Finding out the relationship between these two is a lot like finding the difference between absolute and apparent magnitudes. If we know two of the three values (luminosity, observed brightness, and distance), we should be able to find the third. The peak luminosity of all type Ia supernovae is 1.60×1036 Watts. If we see a star go supernova from earth, and we observe its intensity to be 1.0 W/m2, how far away is this star? Hint: As the light spreads out, it forms a sphere.
Solution
You may notice that the units of luminosity (Watts) are very close to the units of intensity (Watts/m2). The intensity of an object takes the total luminosity and spreads it out over a wider area. When light leaves a source, it goes evenly in all directions, making a sphere of light that finally hits the observer. This tells us that I, intensity, is equal to L, luminosity, over the area of a sphere:
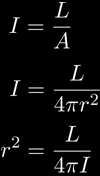
Giving us a nice result for the distance, r. Notice how above, I is inversely proportional to one over the distance squared.
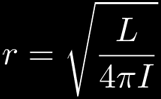
Plugging in our numbers:
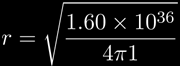
and we see that r=1.1×1017 m, or 11.6 light years.