The Inverse Square Law

So what's the big deal with this "inverse square" we keep talking about? The planets in our solar system are all in roughly circular orbits, driven around the sun by gravity. Since gravity follows an inverse square relationship, the planets that are further from the sun experience significantly less force than those nearer to the sun. The force of gravity, as you may remember from earlier in the site, is given by the following equation:

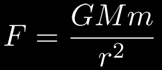
How does force on a planet affect its speed? Is there a relationship between how far away a planet is from the sun and how fast it orbits?

Solution

We can use Newton's second law, F = ma, to find out. Since the orbits of the planets are pretty much circles, we can use centripetal acceleration to obtain the velocities:

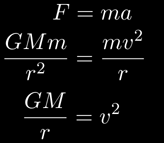
This is the result from our inverse square force -- unlike stars in the galaxy, which orbit the center of the galaxy at roughly equal speeds, a planet's speed gets smaller as r, the distance from the sun, gets bigger:

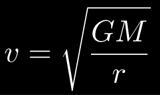
This is the same results that cosmologists expected to get when they studied the stars' motion about the center of the galaxy. Instead, they found that the velocities don't drop off as r gets bigger. This led some to suggest that there must be more, unknown matter in the universe.